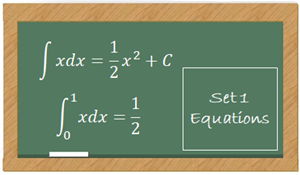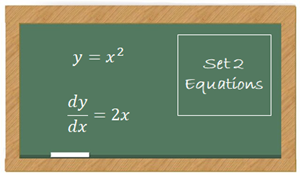Calculus is about slopes and areas
Hold on Tight
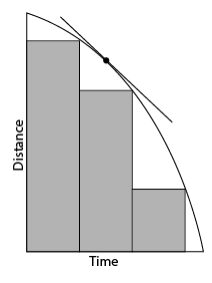
The roller coaster descends in free fall. Seconds later, a picture is taken. The challenge is to find the velocity of the roller coaster at that moment in time.
The graph of distance over time produces a curve. You can find the velocity at a point on the curve by finding the slope of a line that touches the curve at that tangent point. You can do this by looking at the roller coaster position through smaller and smaller intervals of time. Finding the slope of the curve is called differentiation. The slope is the derivative.
You can use rectangles to approximate the area under a curve. As the width of each inscribed rectangle is repeatedly reduced, the number of rectangles increases. When the width gets too small to measure—but never equals zero‑you can find the actual area by adding the areas of all the rectangles. This process is called integration.
Calculus is just about slopes and areas.
Math Class
Excitement builds. The Roller Coaster descends in free fall. Three seconds later a picture is taken with a camera mounted 144 feet from the top.
In math class the students are challenged to find the velocity of the roller coaster at the instant the picture was taken. One student thought this to be an easy problem. Velocity is distance divided by time. Velocity, therefore is 144 feet divided by 3 seconds which equals 48 feet per second. But that is not correct!
The teacher begins by explaining that the 48 feet per second velocity that her student found could only be valid if velocity is constant. On the way down, the roller coaster is in free fall. The velocity is not constant but ever increasing due to gravity.
The teacher explains that a long time ago, a man named Galileo wanted to know how gravity affected the motion of a falling object. He discovered that an object in free fall gains velocity each second at a rate of 32 feet per second. So at the end of one second, the velocity is 32 feet per second. At the end of two seconds, the velocity is 32 times 2 feet per second which is 64 feet per second. If v represents velocity, then v = 32t. We know the time to the picture point to be 3 seconds. So v = 32 times 3 which equals 96 feet per second. The students have found velocity at an instant in time. This is known as the Derivative which is the basic concept of Calculus.
The Goal of Calculus Class Is to Understand These Two Sets of Equations
Students who do will be better prepared for a more rigorous Calculus curriculum later in their math education.